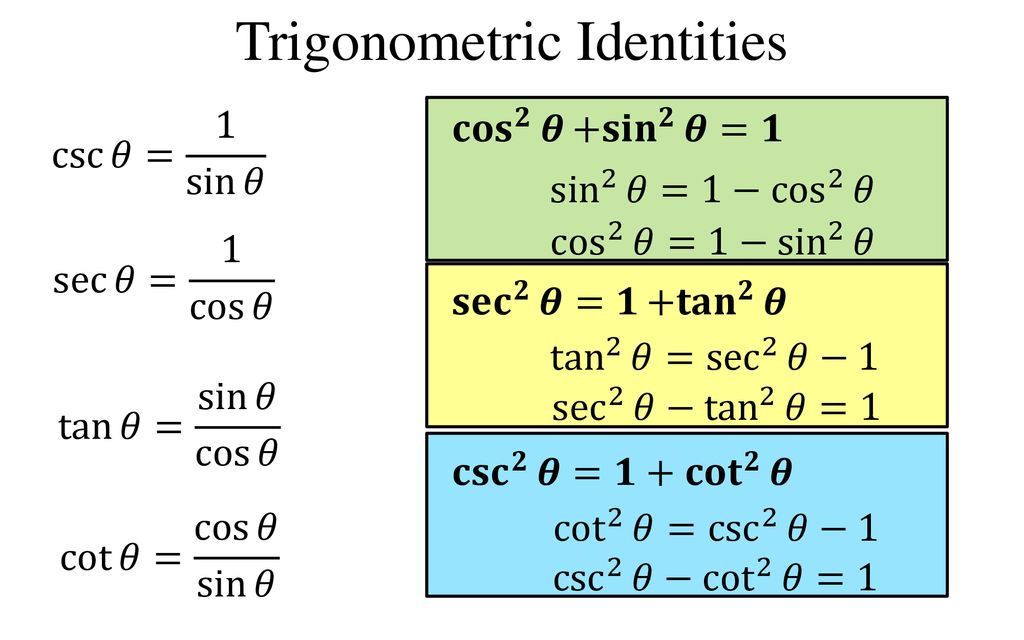
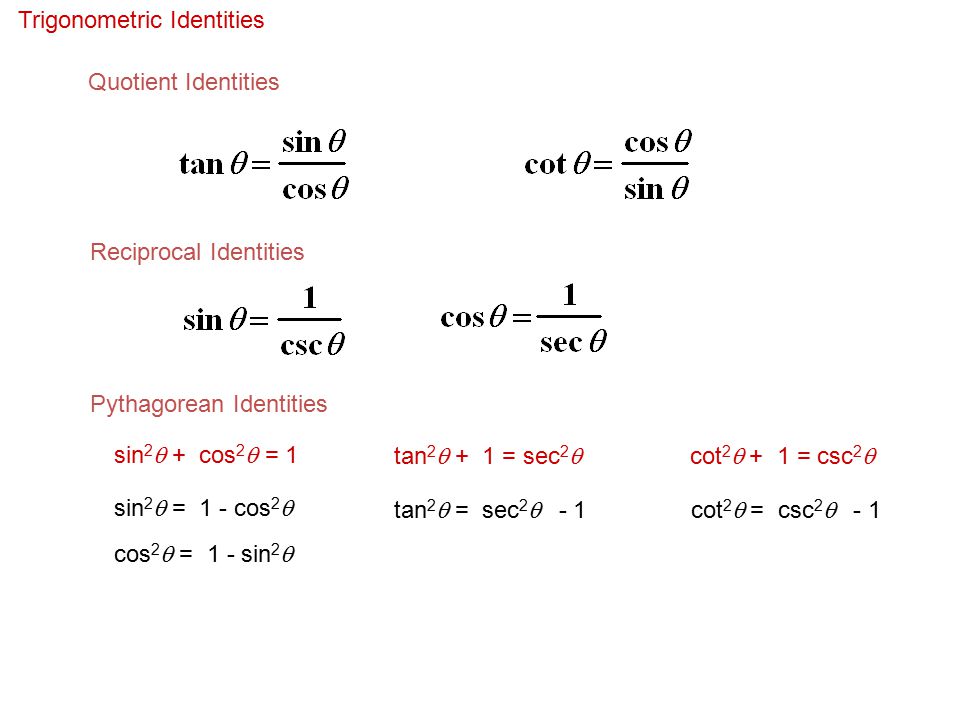
Trigonometry Identities Quotient Identities tan𝜃=sin𝜃 cos𝜃 cot𝜃=cos𝜃 sin𝜃 Reciprocal Identities csc𝜃= 1 sin𝜃 sec𝜃= 1 cos𝜃 cot𝜃= 1 tan𝜃 Pythagorean Identities sin2𝜃cos2𝜃=1 tan 2𝜃1=sec2𝜃 1cot2𝜃=csc2𝜃 Sum & Difference Identities sin( )=sin cos cos sinAs we know, from trigonometry identities, 1tan 2 A = sec 2 A sec 2 A – 1 = tan 2 A (1/cos 2 A) 1 = tan 2 A Putting the value of cos A = ⅘ (5/4) 2 – 1 = tan 2 A tan 2 A = 9/16 tan A = 3/4A cot θ tan θ = 1b sec^2 θ csc^2 θ = 1c tan^2 θ = sin^2 θ x sec^2 θ d cos^2 θ = sec^2 θ x tan^2 θ
How I Remember Trig Identities Part 2 Beyond Solutions
Trigonometric identities tan^2
Trigonometric identities tan^2-Following table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ = 2tanθ 1 tan2θ cos2θ = 1 −tan2θ 1 tan2θTrig identities Trigonometric identities are equations that are used to describe the many relationships that exist between the trigonometric functions Among other uses, they can be helpful for simplifying trigonometric expressions and equations The following shows some of the identities you may encounter in your study of trigonometry




Trigonometry Reciprocal Identities Expii
Trigonometry (from Greek trigōnon, "triangle" and metron, "measure") is a branch of mathematics that studies relationships between side lengths and angles of triangles The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studiesCos^2 x sin^2 x = 1 sin x/cos x = tan x You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more some other identities (you will learn later) include cos x/sin x = cot x 1 tan^2 x = sec^2 x 1 cot^2 x = csc^2 x hope this helped!TRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u
This article uses the notation below for inverse trigonometric functions Function sin cos tan sec csc cot Inverse arcsin arccos arctan arcsec arccsc arccot Pythagorean identity The basic relationship between the sine and the cosine is the Pythagorean trigonometric identity where cos2 θ means (cos(θ))2 and sin2 θ means (sin(θ))2Tan — tan2Ð — cot2Ð sec2Ð csc2Ð Use Trigonometric Identities to write each expression in terms of a single trigonometric identity cos2Ð sine pulatz or a constant a tan cose L8Sfr c cos cscÐ sin sec e tan e 35 Example 2 15 Simplify the complex fractionDefinition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p
Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 while tangent θ = 2 3 − 5 3 = − 2 5 = − 2 5 5 Find the values of the other five trigonometric functions Example 321 2 tan θ = − 5 12, π 2 < θ < π Solution First, we know that \theta is in the second quadrant, making sine positive and cosine negative For this problem, we will use the Pythagorean Identity 1 tan 2The other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions if the argument is regarded as an angle given in radians




14 2 Trigonometric Identities
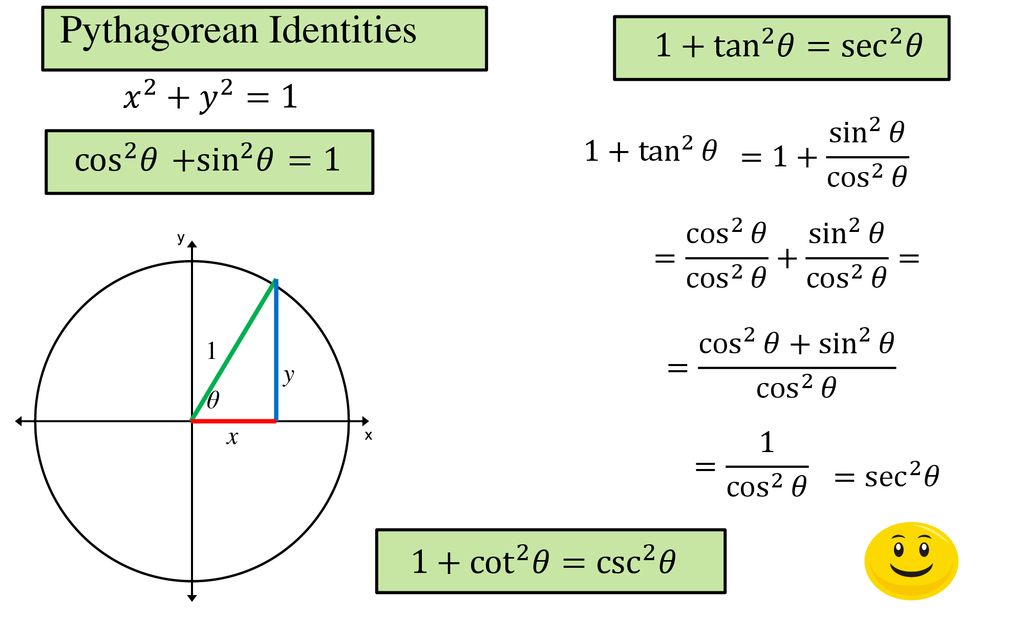



Trigonometric Identities And Equations Ppt Download
(x 5)(x − 5) = x 2 − 25 The significance of an identity is that, in calculation, we may replace either member with the other We use an identity to give an expression a more convenient form In calculus and all its applications, the trigonometric identities are of central importance On this page we will present the main identitiesC2 Trigonometry Trigonometric Identities PhysicsAndMathsTutorcom Edexcel Internal Review 1 1 Solve, for 0 < θ < 360°, giving your answers to 1 decimal place where appropriate, (a) 2 sin θ = 3 cos θ, (3) (b) 2 – cos θ = 2 sin2 θ (6) (Total 9 marks) 2 Solve, for –90° < x < 90°, giving answers to 1 decimal place, (a) tan (3xThe functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is defined




Trigonometry Reciprocal Identities Expii



Http Tutorial Math Lamar Edu Pdf Trig Cheat Sheet Pdf
The secant, cotangent, and cosecant are all reciprocals of other functions The secant is the reciprocal of the cosine function, the cotangent is the reciprocal of the tangent function, and the cosecant is the reciprocal of the sine function The six trigonometric functions can be found from a point on the unit circleThe key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplified2 The Elementary Identities Let (x;y) be the point on the unit circle centered at (0;0) that determines the angletrad Recall that the de nitions of the trigonometric functions for this angle are sint = y tant = y x sect = 1 y cost = x cott = x y csct = 1 x These de nitions readily establish the rst of the elementary or fundamental identities given in the table below
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Tangent Half Angle Formula Wikipedia
Cot (x) = cot (x) sin 2 (x) cos 2 (x) = 1 tan 2 (x) 1 = sec 2 (x) cot 2 (x) 1 = csc 2 (x) sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x)This is one of the Pythagorean identities In the same way, we can derive two other Pythagorean trigonometric identities 1tan 2 θ = sec 2 θ;1tan 2 a = sec 2 a As it is known that tan a is not defined for a = 90° therefore identity 2 obtained above is true for 0 ≤ A



Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero
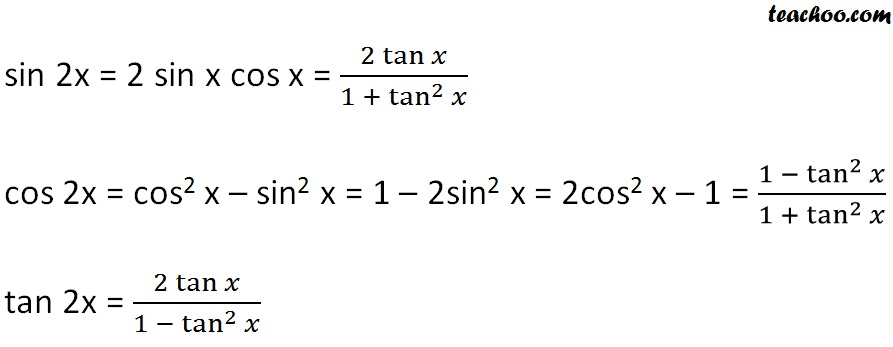



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
TRIGONOMETRIC IDENTITIES By Joanna GuttLehr, Pinnacle Learning Lab, last updated 5/08 Pythagorean Identities sin (A) cos (A) 1 1 tan (A) sec (A) 1 cot (A) csc2 (A)Quotient Identities sin( )2 Prove that Sec 2 P tan 2 P Cosec 2 P Cot 2 P = 0 Solution Sec 2 P tan 2 P Cosec 2 P Cot 2 P = 1 tan 2 P tan 2 P (1 Cot 2 P) Cot 2 P = 1 0 1 Cot 2 P Cot 2 P = 0 Fun Facts Trigonometric identities are true for all the angles between 0 0 and 90 0 With the help of these basic trigonometric identities, manyProving a Trigonometric Identity Prove the trigonometric identity 1\tan ^{2} \theta=\sec ^{2} \theta 💬 👋 We're always here Join our Discord to connect with other students 24/7, any time, night or



Verifying Trigonometric Identities How To Do It The Easy Way Lesson Plan Spiral




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic
Trigonometricidentityprovingcalculator prove \tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) enPeriodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosine The cofunction identities are summarized in Table 722 Table 722 sinθ = cos(π 2 − θ) cosθ = sin(π 2 − θ) tanθ = cot(π 2 − θ) cotθ = tan(π 2 − θ) secθ = csc(π 2 − θ) cscθ = sec(π 2 − θ) Notice that the formulas in the table may also justified algebraically using the sum and difference formulas




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
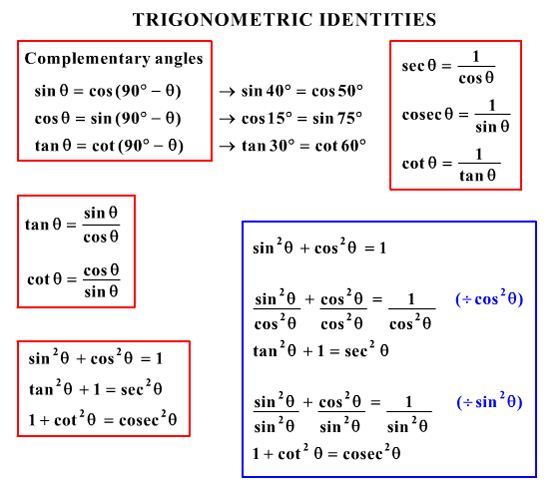



How To Solve Tan 2y Sec 2y Tan 4y Tan 2y Socratic
1cot 2 θ = cosec 2 θSection 71 Solving Trigonometric Equations and Identities 413 Try it Now 2 Solve 2 2sin ( ) 3cos(t t ) for all solutions t 0 2 In addition to the Pythagorean identity, it is often necessary to rewrite the tangent, secant,Start studying Trigonometric Identities Pt 2 Learn vocabulary, terms, and more with flashcards, games, and other study tools
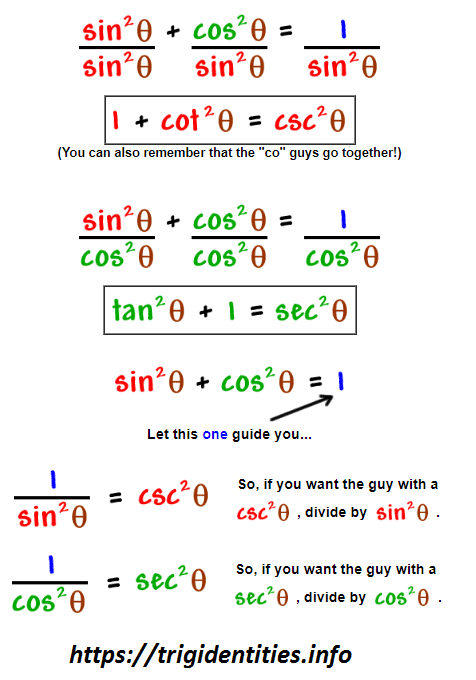



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities




Tangent Half Angle Formula Wikipedia
No matter how big or small the triangle is When we divide Sine by Cosine we get sin (θ) cos (θ) = Opposite/Hypotenuse Adjacent/Hypotenuse = Opposite Adjacent = tan (θ) So we can say tan (θ) = sin (θ) cos (θ) That is our first Trigonometric Identity θ = tan − 1(x)isequivalenttox = tanθ sin(sin − 1(x)) = x cos(cos − 1(x)) = x tan(tan − 1(x)) = x sin − 1(sin(θ)) = θ cos − 1(cos(θ)) = θ tan − 1(tan(θ)) = θ Given below are some more inverse trigonometry formulas sin 1 (x) = – sin 1 xIn this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig id



Trigonometric Identities And Equations Ppt Download




Tangent Identities
The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle and determine whether the identity is odd or even (See Table 2 ) EvenOdd Identities tan( − θ) = − tan θ cot( − θ) = − cot θ sin( − θ) = − sin θTrigonometry is the branch of mathematics which is basically concerned with specific functions of angles, their applications and their calculations In mathematics, there are a total of six different types of trigonometric functions Sine (sin), Cosine (cos), Secant (sec), Cosecant (cosec), Tangent (tan) and Cotangent (cot)To determine the difference identity for tangent, use the fact that tan(−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan x The preceding three examples verify three formulas known as the reduction




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
Trigonometric cofunction identities are relationships between the basic trigonometric functions (sine and cosine) based on complementary anglesThey also show that the graphs of sine and cosine are identical, but shifted by a constant of π 2 \frac{\pi}{2} 2 π The identities are extremely useful when dealing with sums of trigonometric functions, as they often allow for use of the The following are the identities of inverse trigonometric functions sin 1 (sin x) = x provided – π /2 ≤ x ≤ π /2 cos 1 (cos x) = x provided 0 ≤ x ≤ π tan 1 (tan x) = x provided – π /2 < x < π /2 sin (sin 1 x) = x provided 1 ≤ x ≤ 1 cos (cos 1 x) = x provided 1 ≤ x ≤ 1 tan (tanTrigonometric Identities Given $\tan(2a)=2$ and $\frac{3\pi}{2}




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




Summary Of Trigonometric Identities
Trigonometric Identities cos^2 A sin^2 A = 1 1 tan^2 A = sec^2 A cot^2 A 1 = cosec^2A We will prove the above trigonometric identities via a Δ ABC, rightangled at B To learn how to prove Trigonometric Identities, watch the video 👇🏻 Which of the following is a trigonometric identity?Trigonometric Identities Worksheet I Prove each identity 1) tanxcos x = sinx 2) cotxsec x = esc x 3) sin x cot x == cos x 4) tan xcsc x sec



Double Angle And Multiple Angle Identities
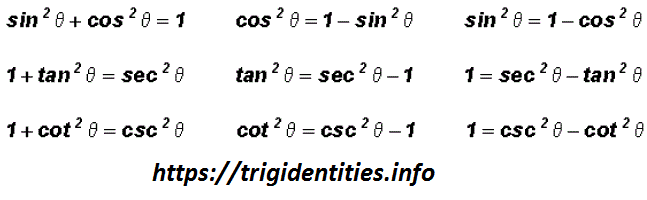



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities
Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x /cos x equation 1Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics trigonometricequationcalculator Tan^{2} en Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions ) Explanation We will use the identity tanθ = 2tan(θ 2) 1 − tan2(θ 2) Let x = tan(θ 2) then tanθ = 2x 1 −x2 or tanθ(1 −x2) = 2x or −tanθx2 −2x tanθ = 0 or tanθx2 2x − tanθ = 0 Now using quadratic formula x = −2 ± √22 − 4 × tanθ ×( − tanθ) 2tanθ x = −2 ± √4 4tan2θ 2tanθ or




Verifying Trigonometric Identities Sec 7 1 Trigonometric Expression Identity
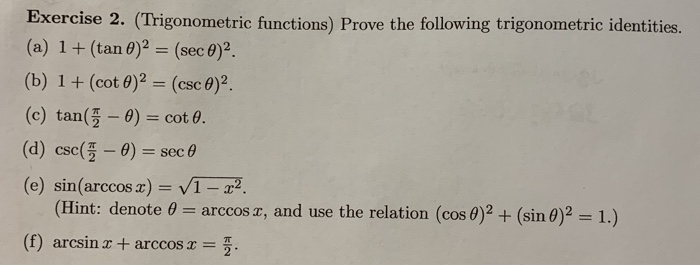



Exercise 2 Trigonometric Functions Prove The Chegg Com
Math Trigonometry Trigonometry questions and answers O TRIGONOMETRIC IDENTITIES AND EQUATIONS Halfangle identities Problem type 2 1 Suppose that tan a 11 and 90°




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Exercise Set 4 4 Trigonometric Expressions And Identities Math 1330 Docsity




14 2 Trigonometric Identities




5 2 Verifying Trigonometric Identities Copyright Cengage Learning




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Math34 Trigonometric Formulas




Summary Of Trigonometric Identities
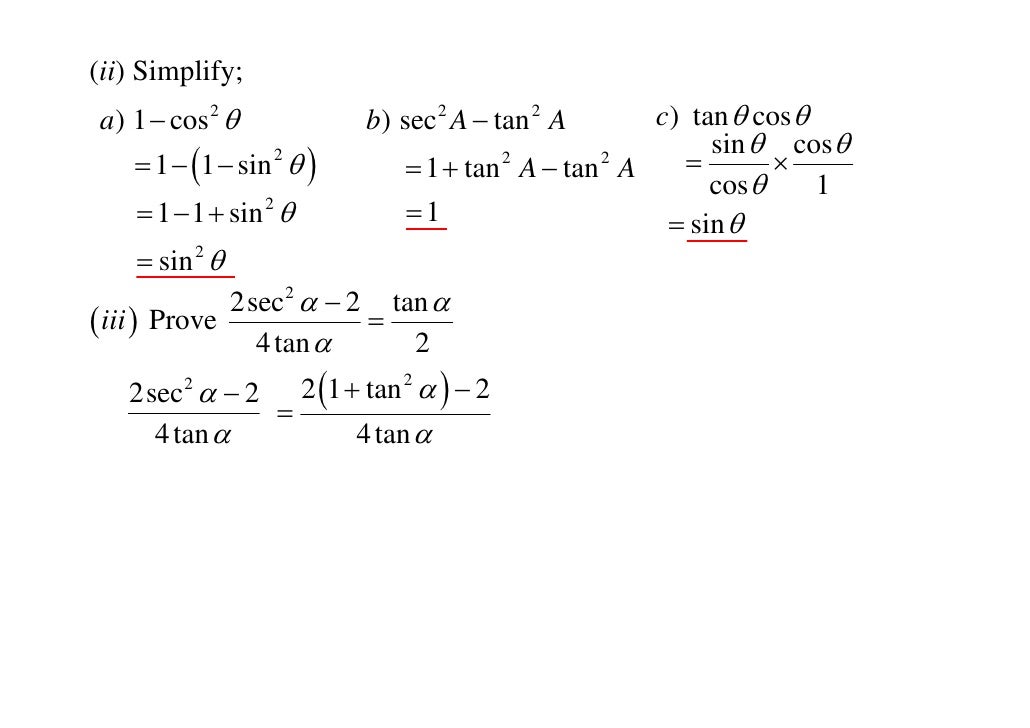



11 X1 T04 03 Pythagorean Trig Identities 10




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube



3



Trigonometric Identities Examples




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Using Standard Trigonometric Identities Show That Chegg Com




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube




6 2 Trigonometric Identities Trigonometry Siyavula




Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download




Trigonometric Identities List Of Trigonometric Identities Examples
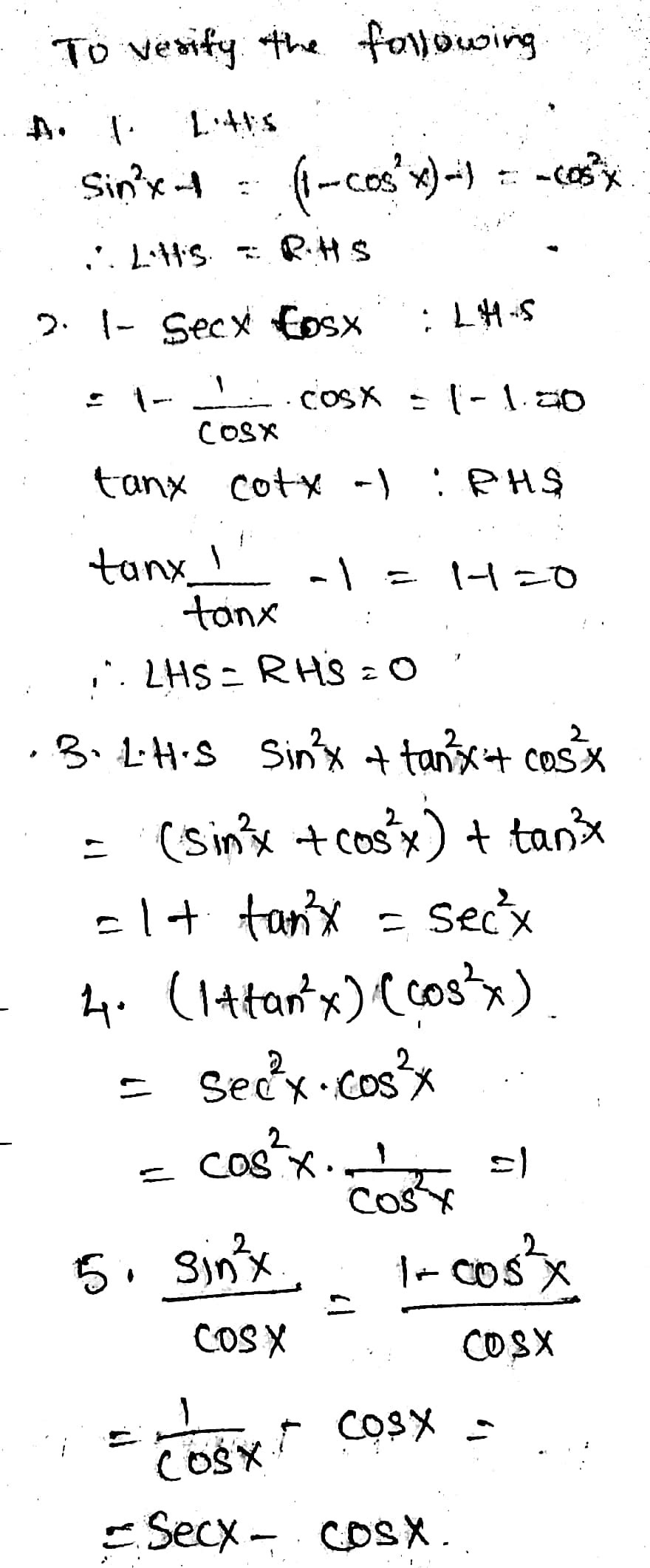



Directions Verify The Following Trigonometric Id Gauthmath




Cos Sin Tan Csc Sec Cot




Trigonometric Identities List Of Trigonometric Identities Examples




Use Trigonometric Identities To Solve Each Equation In The Interval 0 21 C X 2 Tan 2x Homeworklib




How To Use Double Angle Identities Studypug




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



Trigonometric Identities



Cofunction And Reduction Identities



Derivatives Of Trigonometric Functions
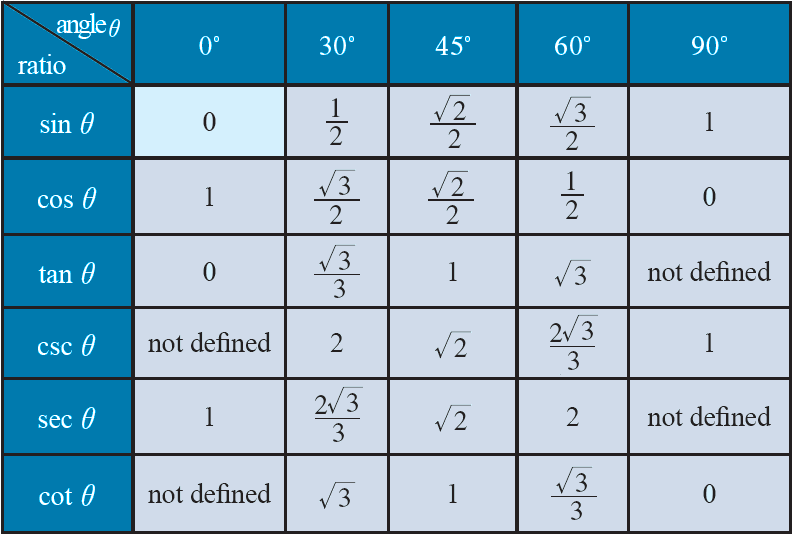



Trigonometric Identities




Integrate Sec 2x Method 1



Www Brockport Edu Academics Tutoring Docs Trigonometric Identities Pdf




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Solved 4 A Evaluate 27 2 C 1 Dx 1 22 You May Use Chegg Com




5 2 Verifying Trigonometric Identities Copyright Cengage Learning




We Wish To Prove The Following Trig Identity Tan X Chegg Com




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Prove The Following Trigonometric Identities Show Gauthmath




List Of Trigonometric Identities Wikipedia
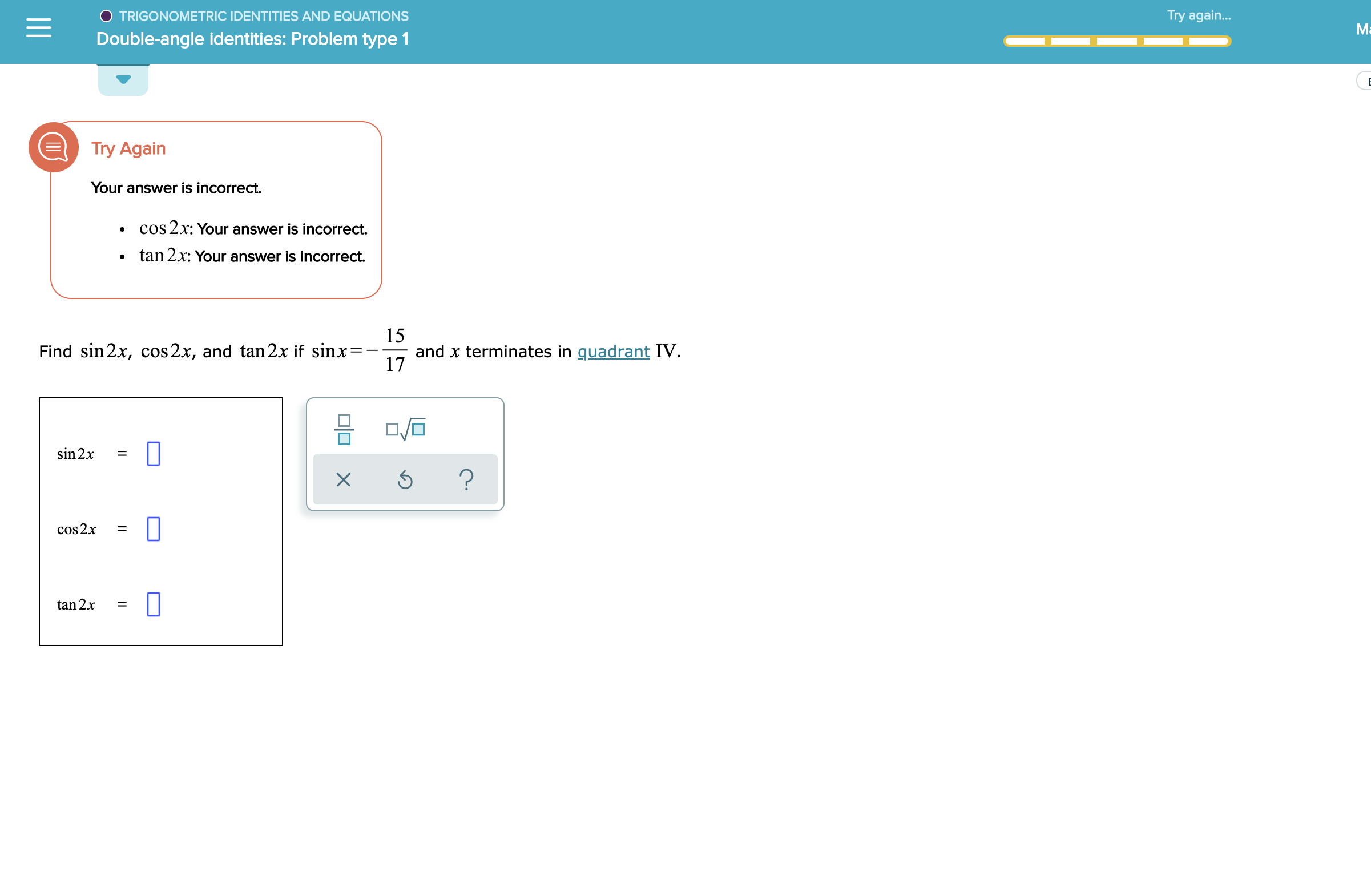



Answered O Trigonometric Identities And Bartleby



Cofunction And Reduction Identities
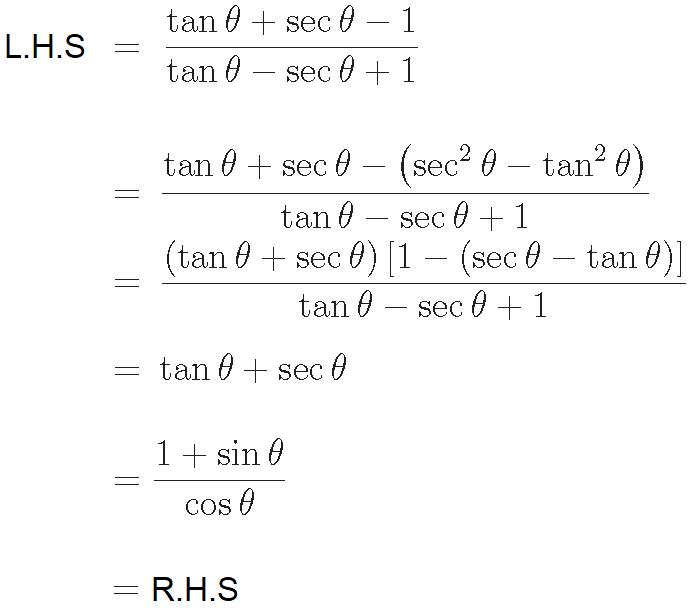



Basic Trigonometric Identities




Cos Sin Tan Csc Sec Cot




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



1



Derivatives Of Trigonometric Functions Web Formulas




Trigonometric Identities December 10 Remember Y Sin
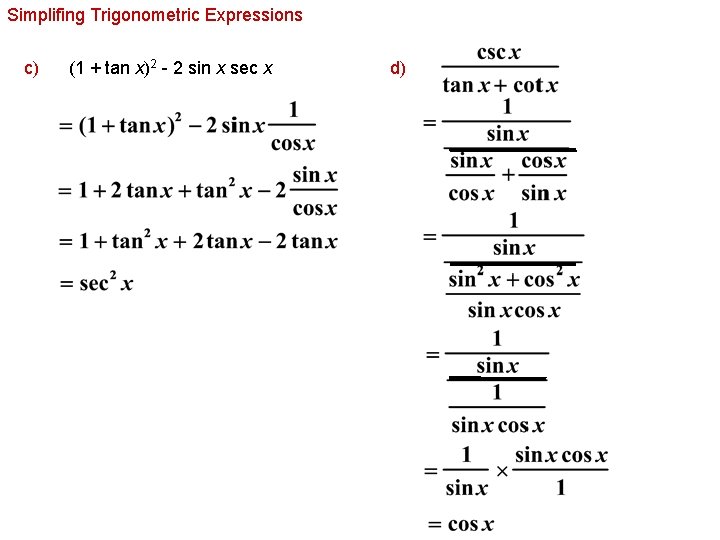



While You Wait Trigonometric Identities And Equations Section




Powers Of Trigonometric Functions




Ohui9rfcymv4bm
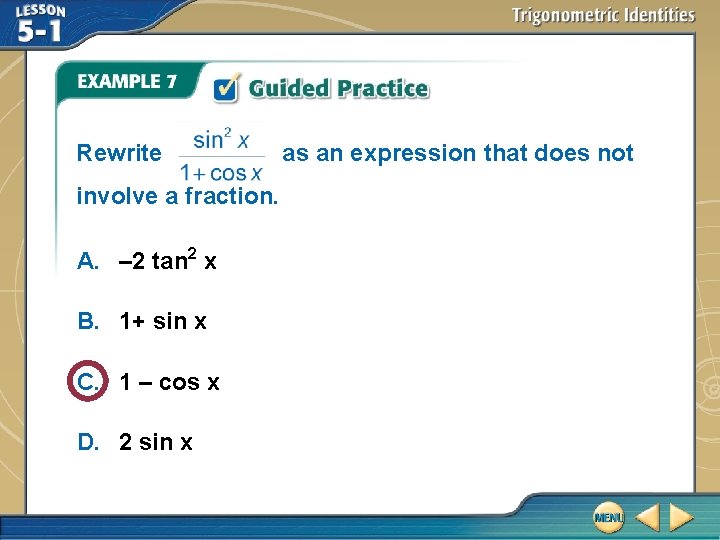



Lesson 5 1 Trigonometric Identities Fiveminute Check Over



What Are The Quotient Identities For A Trigonometric Functions Socratic




Trigonometric Identities Proofs List Of All Trig Identities




Summary Of Trigonometric Identities



How I Remember Trig Identities Part 2 Beyond Solutions
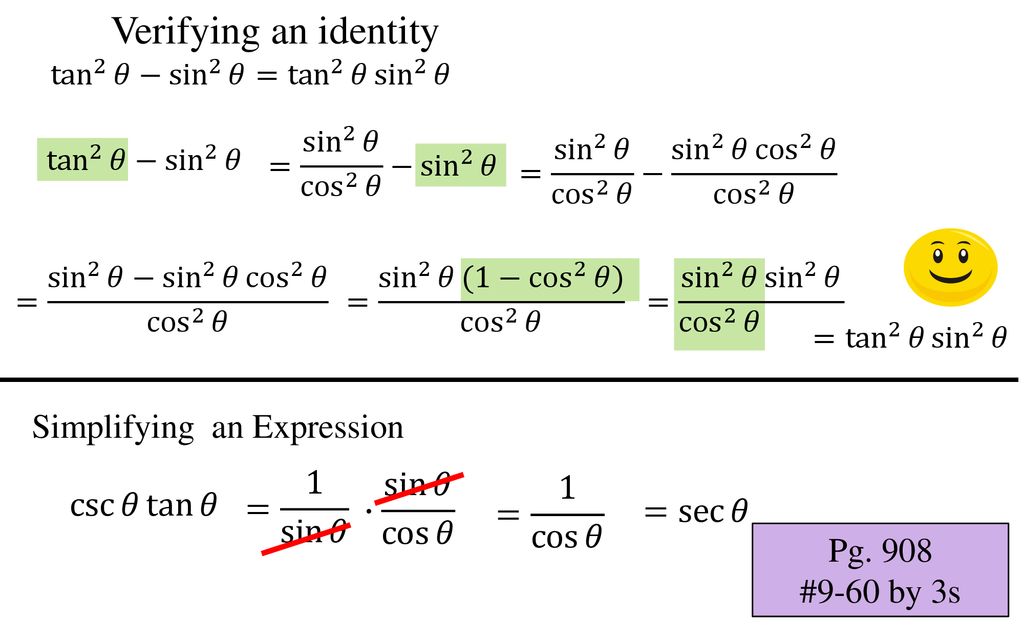



Trigonometric Identities And Equations Ppt Download



1



What Is The Formula Of Tan2x Quora




Trigonometry Mind42



Cos Sin Tan Csc Sec Cot




Trigonometric Identities And Examples With Worksheets




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube
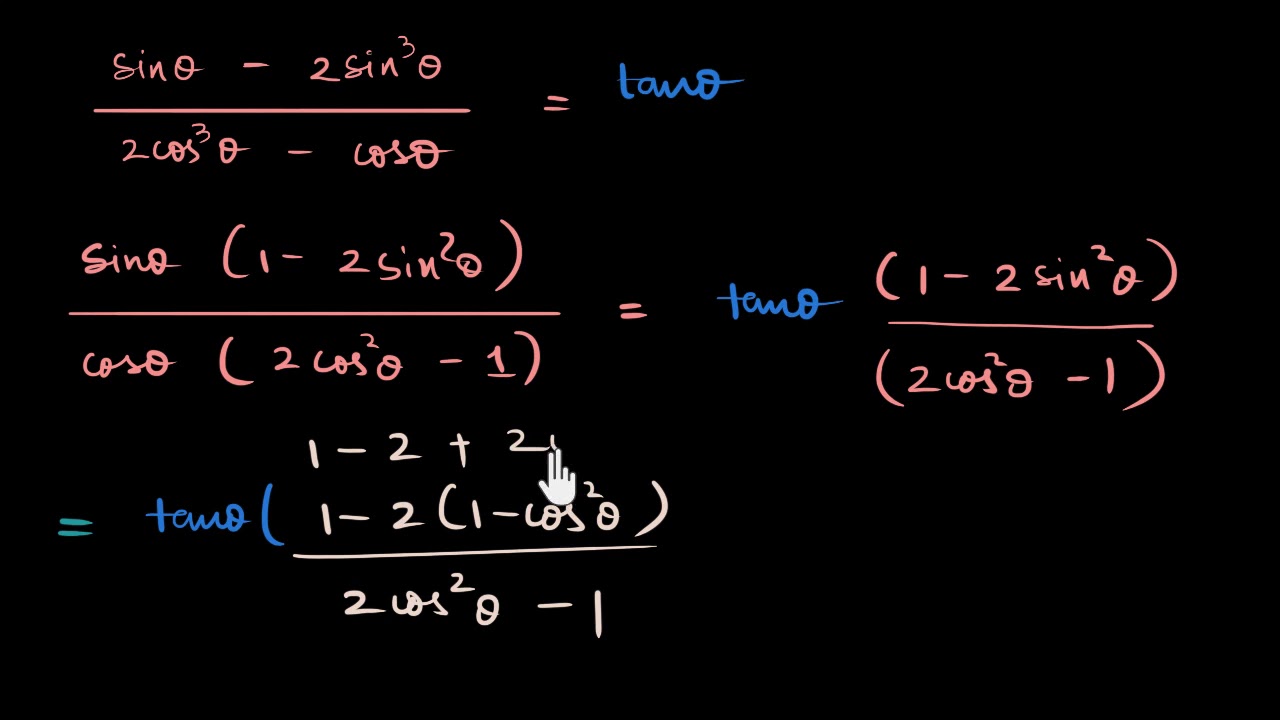



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy




Tan 2x Formula What Is Tan 2x Formula Examples
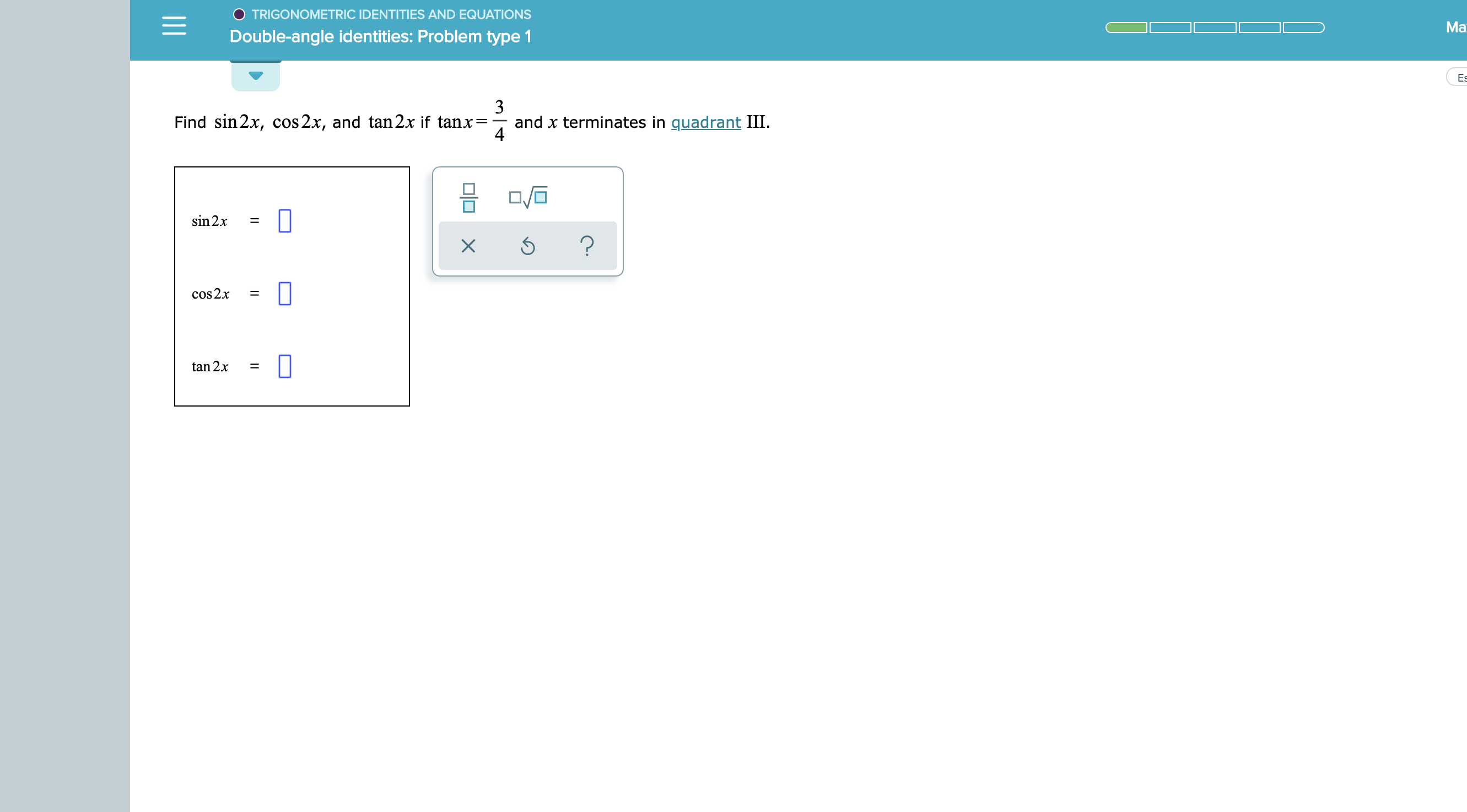



Answered O Trigonometric Identities And Bartleby




Trigonometric Identities Trigonometric Functions Trigonometry



1




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




Worksheet On Trigonometric Identities Establishing Identities Hints




Integrate Sec 2x Method 2



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



Cos2x Identity




Trigonometric Identities A Plus Topper




Lesson 22 Trigonometric Identities Ib Math Hl




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions
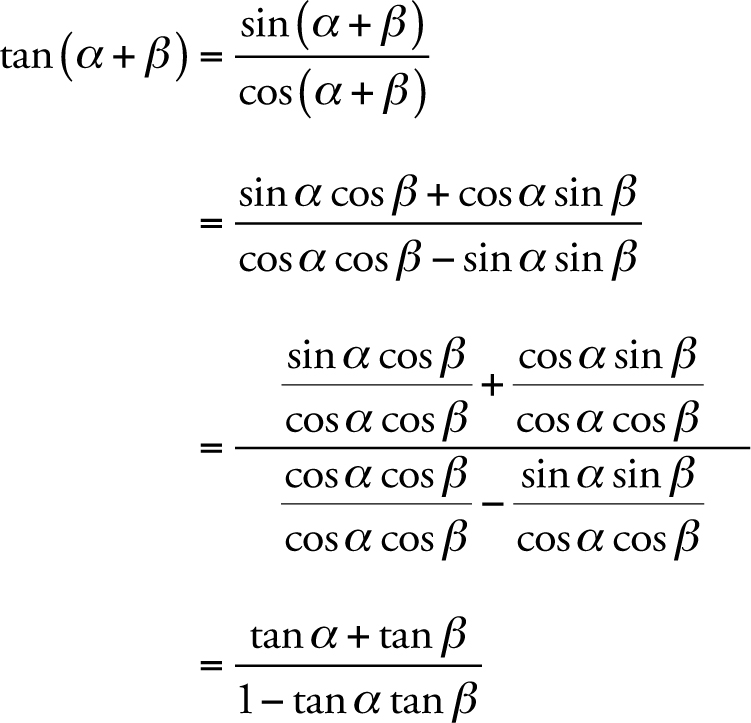



Tangent Identities




Math34 Trigonometric Formulas




Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



0 件のコメント:
コメントを投稿